介绍
Splay 树 是一种平衡二叉树,实现比较简单,可以在均摊复杂度$log(n)$对树进行修改和查询。在学这个之前得知道什么是二叉搜索树,二叉搜索树很简单,就是在树上不断把比他大的儿子往右边放,把比他小的儿子往左边放。很显然这种策略是可以被卡到$O(n)$的复杂度,所以就出现对这颗树进行修改的平衡二叉树,Splay 树就是其中一种
实现
实现网上已经有很多了,我根据自己理解,写一些记录。
先说一下基础的
首先是定义变量1
2
3
4
5
6int ch[maxn][2];//左右儿子
int fa[maxn]; //父亲
int size[maxn]; //字树大小
int cnt[maxn]; //关键字出现次数
int key[maxn]; //关键字
int sz,root; // 树的大小 根节点
然后是几个简单的函数,清除和判断是不是右儿子1
2
3
4
5
6
7inline void clear(int x){
ch[x][0]=ch[x][1]=fa[x]=size[x]=cnt[x]=key[x];
}
inline int get(int x){
return ch[fa[x]][1]==x;
}
因为更新之后节点的左右儿子会变,所以就顶一个更新函数1
2
3
4
5
6
7
8
9inline void update(int x){
if(x){
size[x]=cnt[x];
if(ch[x][0])
size[x]+=size[ch[x][0]];
if(ch[x][1])
size[x]+=size[ch[x][1]];
}
}
核心算法: rotate,旋转操作。选择也很简单,在网上盗了大佬的图。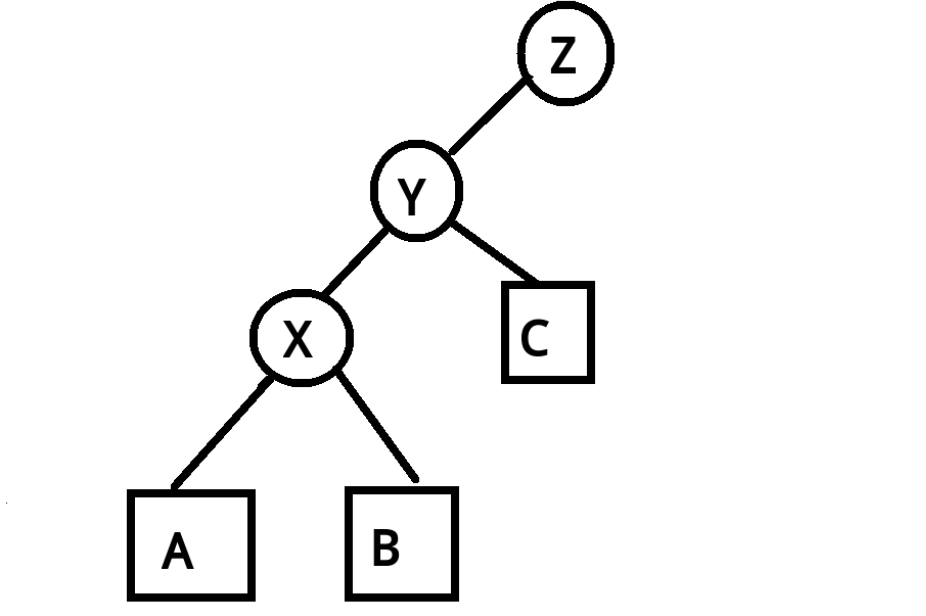
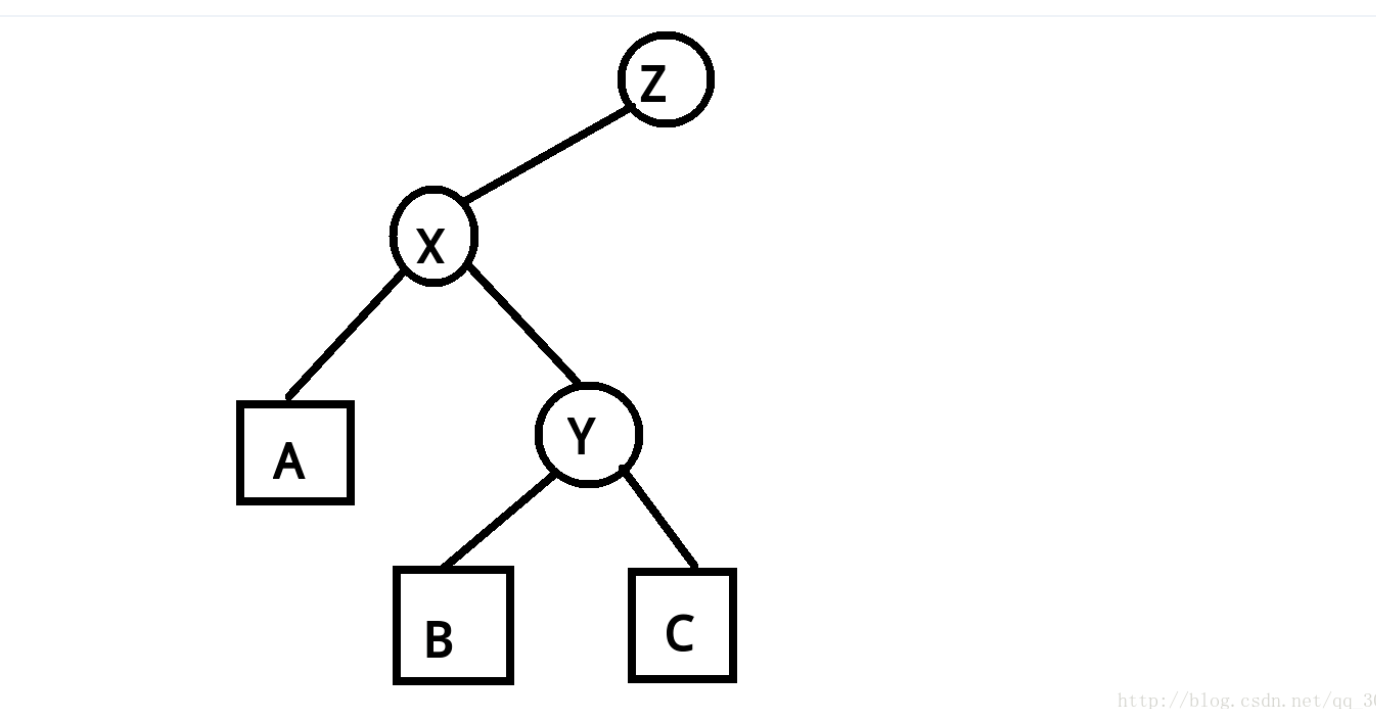
看了这两个图,应该就明白了吧,旋转就是这么简单。如果是右儿子就要换一下旋转。1
2
3
4
5
6
7
8
9
10
11
12inline void rotate(int x){
int old=fa[x],oldf=fa[old],which=get(x);
ch[old][which]=ch[x][which^1]; // 是做儿子 把自己右儿子 给父亲的左耳子 否则反之
fa[ch[old][which]]=old; // 把交换的儿子父亲设置成父亲
fa[old]=x; //把父亲节点变儿子节点
ch[x][which^1]=old;
fa[x]=oldf; //把自己父亲设置成父亲的父亲
if (oldf)
ch[oldf][ch[oldf][1]==old]=x; // 变成父亲的父亲节点的儿子
update(old);update(x);
}
然后就是伸展操作,这个算法能实现 均摊$O(log(n))$的复杂度,靠的就是这个。
每次查询一个值,通过不断的rotate 把他变为根节点,同样,每次查询都会把路径上的深度减小。这个自己画个图理解一下。。。。1
2
3
4
5
6inline void splay(int x){
for (int p;(p=fa[x]);rotate(x))
if (fa[p])
rotate((get(x)==get(p)?p:x));// 判断三点共线就先选择父亲,保证消减深度
root=x;
}
这地方理解了后面就都是打酱油的角色了。
查找1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16inline int find(int v){
int ans=0,now=root;
while (1){
if (v<key[now]) //如果小于 就往左找
now=ch[now][0];
else{
ans+=(ch[now][0]?size[ch[now][0]]:0) //大于加上左子树的大小
if (v==key[now]) {
splay(now);
return ans+1;
}
ans+=cnt[now];
now=ch[now][1];
}
}
}
查询第 x 小1
2
3
4
5
6
7
8
9
10
11
12
13inline int findx(int x){
int now=root;
while (1){
if (ch[now][0]&&x<=size[ch[now][0]])
now=ch[now][0];
else{
int temp=(ch[now][0]?size[ch[now][0]]:0)+cnt[now];
if (x<=temp)
return key[now];
x-=temp;now=ch[now][1];
}
}
}
插入1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35inline void insert(int x){
if(root==0){ //root=0相当于 建树
sz++;
ch[sz][0]=ch[sz][1]=fa[sz]=0;
key[sz]=x;
cnt[sz]=1;
size[sz]=1;
root=sz;
return;
}
int now=root,p=0;
while (1){
if(key[now]==x){ //如果已经存在就直接+1
cnt[now]++;
update(now);
update(p);
splay(now);
break;
}
p=now;
now=ch[now][key[now]<x];
if (now==0){ //如果不存在就建一个节点
sz++;
ch[sz][0]=ch[sz][1]=0;
key[sz]=x;
size[sz]=1;
cnt[sz]=1;
fa[sz]=p;
ch[p][key[p]<x]=sz;
update(p);
splay(sz);
break;
}
}
}
查询前驱和后继1
2
3
4
5
6
7
8
9
10
11inline int pre(){
int now=ch[root][0];
while (ch[now][1]) now=ch[now][1];
return now;
}
inline int next(){
int now=ch[root][1];
while (ch[now][0]) now=ch[now][0];
return now;
}
删除操作
这个地方解释一下,有两个儿子的情况,首先find 把值直接提到根节点,如果要删除这个节点,也就是这个值的个数是1的情况,这个时候直接把他的前驱提到根节点,然后删了原来那个节点。 把前驱提到根节点最后一定是下图,要删除的那个点一定没有左儿子,所以可以直接删除。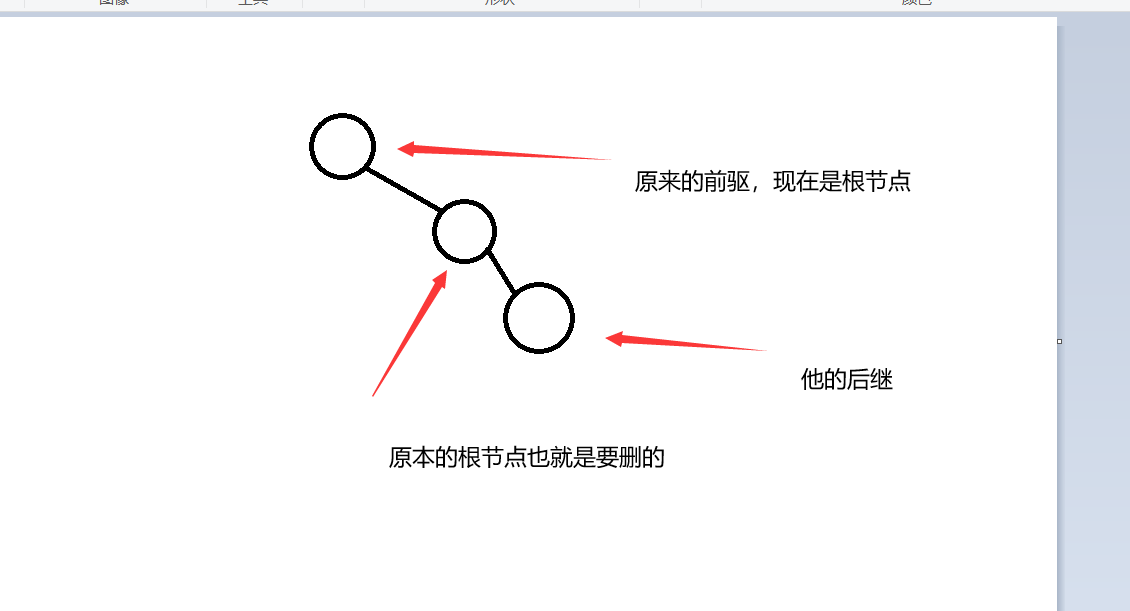
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25inline void del(int x){
int whatever=find(x);
if (cnt[root]>1) {cnt[root]--;update(root);return;}
//Only One Point
if (!ch[root][0]&&!ch[root][1]) {clear(root);root=0;return;}
//Only One Child
if (!ch[root][0]){
int oldroot=root;
root=ch[root][1];
fa[root]=0;
clear(oldroot);
return;
}
else if (!ch[root][1]){
int oldroot=root;root=ch[root][0];fa[root]=0;clear(oldroot);return;
}
//Two Children
int leftbig=pre(),oldroot=root;
splay(leftbig);
fa[ch[oldroot][1]]=root;
ch[root][1]=ch[oldroot][1];
clear(oldroot);
update(root);
return;
}