斜率优化DP

发表于 | 更新于 | 分类于 ， | 阅读次数：
本文字数： 90 | 阅读时长 ≈ 1 分钟

什么是斜率优化DP？顾名思义，用斜率优化的DP。
推荐一波博客这个大哥将的不错。
斜率优化DP，一开始会化成一个式子，像

满足这个式子可以得到$j$转移比$x$转移要优，其中不出意外，$s(i)$是递增的。把这个式子画在图上就是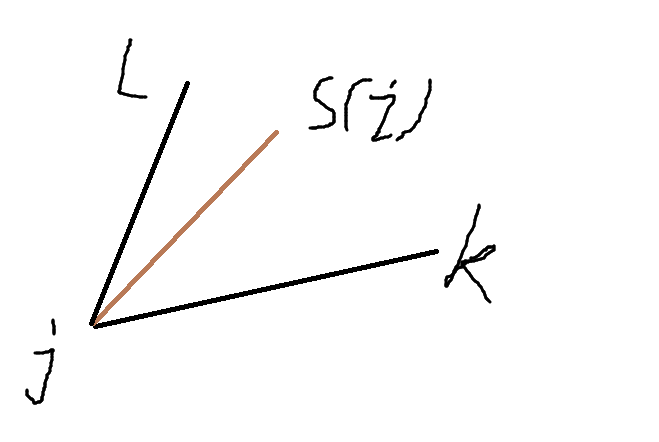

$j,k,l$向$i$转移$j$优于$l$,$k$优于$j$。
利用这个性质我们，保存一个斜率递增的优先队列。，然后队首第一个节点就是转移的最优解。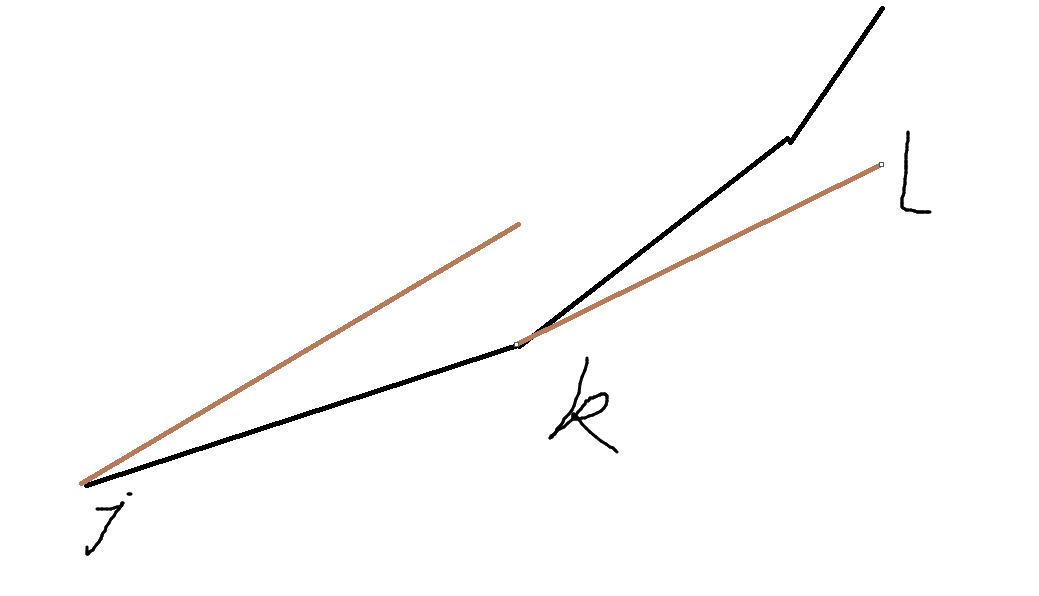

不难看出上图，$k$点最优。
学习例题: HDU 3507

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
#include "bits/stdc++.h"

using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int, int> P;
#define VNAME(value) (#value)
#define bug printf("*********\n");
#define debug(x) cout<<"["<<VNAME(x)<<" = "<<x<<"]"<<endl;
#define mid ((l + r) >> 1)
#define chl 2 * k + 1
#define chr 2 * k + 2
#define lson l, mid, chl
#define rson mid + 1, r, chr
#define eb(x) emplace_back(x)
#define pb(x) emplace_back(x)
#define mem(a, b) memset(a, b, sizeof(a));

const LL mod = (LL) 1e9 + 7;
const int maxn = (int) 1e6 + 5;
const LL INF = 0x7fffffff;
const LL inf = 0x3f3f3f3f;
const double eps = 1e-8;

#ifndef ONLINE_JUDGE
clock_t prostart = clock();
#endif

void f() {
#ifndef ONLINE_JUDGE
    freopen("../data.in", "r", stdin);
#endif
}

//typedef __int128 LLL;

template<typename T>
void read(T &w) {//读入
    char c;
    while (!isdigit(c = getchar()));
    w = c & 15;
    while (isdigit(c = getchar()))
        w = w * 10 + (c & 15);
}

template<typename T>
void output(T x) {
    if (x < 0)
        putchar('-'), x = -x;
    int ss[55], sp = 0;
    do
        ss[++sp] = x % 10;
    while (x /= 10);
    while (sp)
        putchar(48 + ss[sp--]);
}

LL a[maxn];
LL s[maxn];
LL dp[maxn];

LL getup(int i, int j) {
    return dp[i] + s[i] * s[i] - dp[j] - s[j] * s[j];
}

LL getdown(int i, int j) {
    return s[i] - s[j];
}

int n, m;

LL getdp(int i, int j) {
    return dp[j] + (s[i] - s[j]) * (s[i] - s[j]) + m;
}

int p[maxn];

int main() {
    f();
    while (scanf("%d%d", &n, &m) != EOF) {
        mem(dp, 0);
        for (int i = 1; i <= n; i++) {
            read(a[i]);
            s[i] = a[i] + s[i - 1];
        }
        int head = 0, tail = 0;
        tail++;
        dp[0] = 0;
        for (int i = 1; i <= n; i++) {
            while (head + 1 < tail && getup(p[head + 1], p[head]) < getdown(p[head + 1], p[head]) * 2 * s[i])head++;
            dp[i] = getdp(i, p[head]);
            while (head + 1 < tail && getup(p[tail - 1], p[tail - 2]) * getdown(i, p[tail - 1]) >=
                                      getup(i, p[tail - 1]) * getdown(p[tail - 1], p[tail - 2]))
                tail--;
            p[tail++] = i;
        }
        printf("%lld\n", dp[n]);
    }
#ifndef ONLINE_JUDGE
    cout << "运行时间:" << 1.0 * (clock() - prostart) / CLOCKS_PER_SEC << endl;
#endif
    return 0;
}

进阶题: J Wood Processing 题解