HDU 6686 Rikka with Travels
题意: 在一颗树上选择两条不相交的路径的可能性有多少,路径长度定义为路径的顶点数。
题解:
初步思考,观察样例可以发现,求的是两条路径的有序对,[2,1],[1,2]不是同一种。我们假设已经知道你选择的一条路径长度为l,只需要找到把这条路径在树中移除,余下的森林的最长路径是多少,假设是$r$,对于长度为$l$的路径有多条,然后分别求出对应的$r$就是贡献,然后将所有的$l$的贡献,求和就是答案。
很显然这么求就对超时,而且也无从下手。那么我们继续优化,对于一颗树,我们每次拆一条边。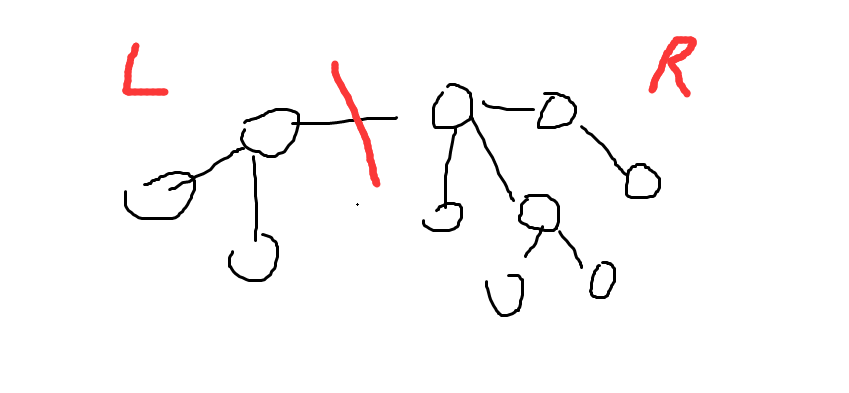
求出左边的最长直径为L,右边的最长直径为R,可以发现左边这颗子树的路径可能有$1,2,\cdots,L$,右边有$1,2,\cdots,R$, 我们可以知道,把区间$l=[1,L]$的贡献跟新为$R$,$l=[1,R]$ 更新为$L$,写出暴力修改就是
对于这个修改暴力肯定是超时的,但是吉老师线段树可以在$O(log^2(n))$的时间内更新。 仔细思考可以发现f[i-1]>=f[i],所以也可以不用吉老师线段树,可以直接 f[l]=max(f[l],R),f[r]=max(L,f[l]),然后做个f[i]=max(f[i],f[i+1]),可以实现一样的结果,复杂度O(1)
对于怎么计算贡献 解决了,下面问题就是怎么求子树的直径了。这个不用看,肯定是 树形DP ,树形DP 保存两个值,一个是这个节点下面叶子最长路径,一个是子树最长路径。最长路径一共有两种情况,一种是经过自己的,一种是来自己某个儿子的。两遍DFS可以解决。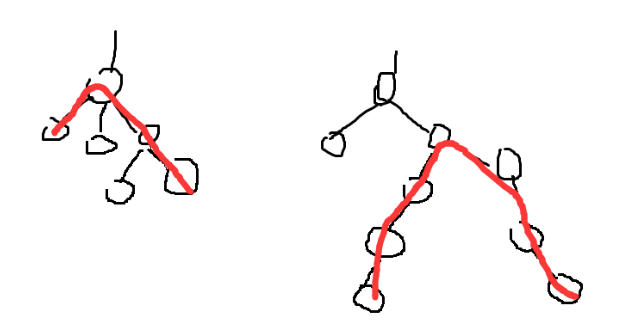
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int, int> P;
const LL mod = (LL) 1e9 + 7;
const int maxn = (int) 1e6 + 5;
const LL INF = 0x7fffffff;
const LL inf = 0x3f3f3f3f;
const double eps = 1e-8;
clock_t prostart = clock();
void f() {
freopen("../data.in", "r", stdin);
}
//typedef __int128 LLL;
template<typename T>
void read(T &w) {//读入
char c;
while (!isdigit(c = getchar()));
w = c & 15;
while (isdigit(c = getchar()))
w = w * 10 + (c & 15);
}
template<typename T>
void output(T x) {
if (x < 0)
putchar('-'), x = -x;
int ss[55], sp = 0;
do
ss[++sp] = x % 10;
while (x /= 10);
while (sp)
putchar(48 + ss[sp--]);
}
int T, n;
vector<int> G[maxn];
int dp[maxn], mx[maxn];
void dfs(int r, int p, int dep) {
for (auto au:G[r]) {
if (au != p) {
dfs(au, r, dep + 1);
dp[r] = max(dp[au], max(dp[r], mx[au] + 1 + mx[r]));
mx[r] = max(mx[au] + 1, mx[r]);
}
}
}
int ans[maxn];
void dfs2(int r, int p, int dep) {
if (p != -1) {
ans[dp[r] + 1] = max(ans[dp[r] + 1], dp[p] + 1);
ans[dp[p] + 1] = max(ans[dp[p] + 1], dp[r] + 1);
}
int mx1 = -1, mx2 = -1, d = -1;
dp[r] = 0;
mx[r] = 0;
for (auto au:G[r]) { //判断 最长直径,最大路径,次短路径在哪
if (mx1 == -1 || d == -1) {
mx1 = au;
d = au;
} else {
if (dp[au] > dp[mx1]) {
d = au;
}
if (mx[au] >= mx[mx1]) {
mx2 = mx1;
mx1 = au;
} else if (mx2 == -1 || mx[au] > mx[mx2]) {
mx2 = au;
}
}
dp[r] = max(dp[au], max(dp[r], mx[au] + 1 + mx[r]));
mx[r] = max(mx[au] + 1, mx[r]);
}
for (auto au:G[r]) { //从根节点更新儿子
if (au == p)continue;
if (au == mx1 || au == mx2 || au == d) {
int tdp = dp[r], tmx = mx[r];
dp[r] = 0;
mx[r] = 0;
for (auto a2:G[r]) {
if (a2 != au) {
dp[r] = max(dp[a2], max(dp[r], mx[a2] + 1 + mx[r]));
mx[r] = max(mx[a2] + 1, mx[r]);
}
}
dfs2(au, r, dep + 1);
dp[r] = tdp;
mx[r] = tmx;
} else {
dfs2(au, r, dep + 1);
}
}
dp[r] = 0;
mx[r] = 0;
for (auto au:G[r]) {//回溯回去重新更新
if (au != p) {
dp[r] = max(dp[au], max(dp[r], mx[au] + 1 + mx[r]));
mx[r] = max(mx[au] + 1, mx[r]);
}
}
}
int main() {
f();
read(T);
while (T--) {
read(n);
for (int i = 0; i < n - 1; i++) {
int u, v;
read(u);
read(v);
G[u].emplace_back(v);
G[v].emplace_back(u);
}
dfs(1, -1, 0);
dfs2(1, -1, 0);
LL res = 0;
for (int i = n - 1; i >= 1; i--) {
ans[i] = max(ans[i], ans[i + 1]);
res = res + ans[i];
// printf("%d%c", ans[i], i == 1 ? '\n' : ' ');
}
printf("%lld\n", res);
for (int j = 0; j <= n; ++j) {
G[j].clear();
ans[j] = 0;
dp[j] = 0;
mx[j] = 0;
}
}
cout << "运行时间:" << 1.0 * (clock() - prostart) / CLOCKS_PER_SEC << endl;
return 0;
}