这个东西学会了AC自动机 理解这个应该不难,AC自动fail指针保存了一个最长匹配后缀,这个也差不多。这个保存了最长匹配后缀回文串。
举个例子
老子找了半天没找到原本看过的博客,只找到了这张图片。随便写几句混一混就过去了。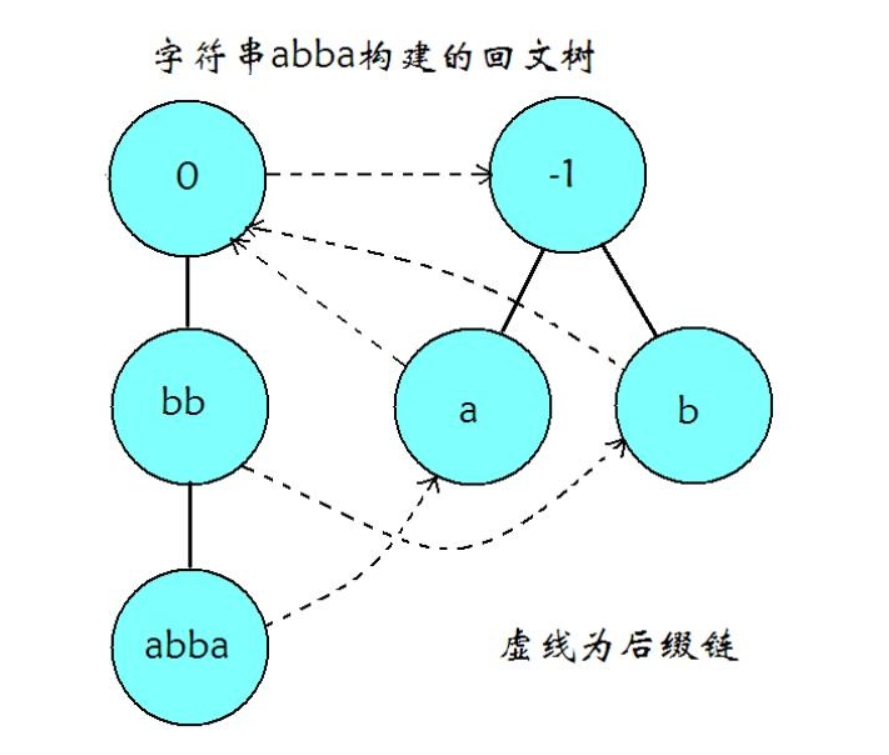
回文树里面的next 和字典树差不多的意义,只不过字典树里面的一个节点是表示在一个节点后面加上一个字符,但next是前后各加一个字符,就是t变成tc 和t变成ctc的区别,前后各加一个字符肯定是回文串。那么问题来了奇数的回文串怎么办,所以出现啊了两个根节点,一个0,一个-1,连在-1的表示是个奇数个数的回文串,看代码里面的x-len[p]+1刚好也是自己,所以自己和自己一定是回文串没啥毛病。再给个图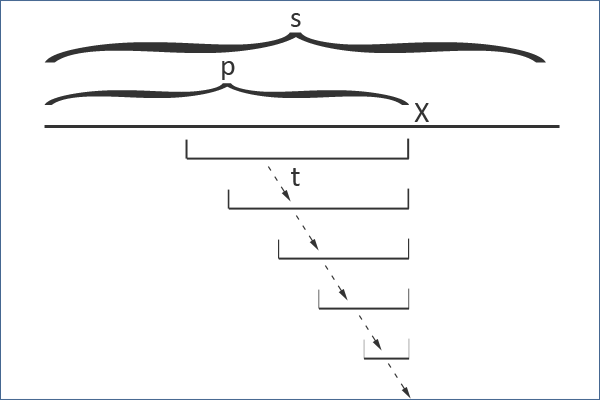
fail差不多就是上图的意思.
解释下例子怎么构造的
开始的时候建立两个根节点,两个根节点一个长度为0,一个-1,将fail[0]=1,0表示长度为0,1号节点长度为-1,一开始加入a肯定是没有任何后缀,直接连上-1根节点,fail肯定是连上0,此时当前节点的回文后缀有a,空串和-1,然后添加b,a节点前面很显然没有b,所以无法匹配,然后匹配空串,空串前面是a所以还是没法匹配,又匹配-1,很显然这个一定是可以的,因为和自己肯定是相同的.也就是构建了这一部分。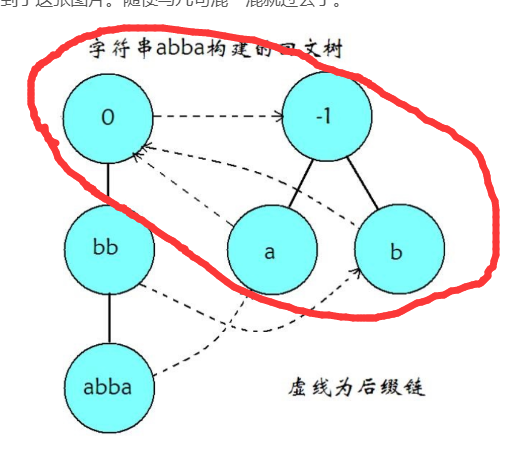
然后下一个字符串还是b,此时后缀有b,空串和-1,匹配后缀b前一个是a很显然不匹配,匹配空串,前一个刚好是b所以此时,将bb连到0节点下面,fail指向父亲节点失陪的第一个能够匹配b的位置,这个有点难理解。
在代码中是这一行。
下一个字符是a,此时字符串最长回文后缀有bb,b,空串和-1,显然bb就直接匹配了,然后再更新fail,差不多就是这么个过程。
多余的不解释看别人博客去吧。
想深入了解,去看看 国家集训队2017年的论文 吧1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61namespace Palindromic_Tree {
const int MAXN = 1000010;
const int N = 26;
int next[MAXN][N];//next指针,next指针和字典树类似,指向的串为当前串两端加上同一个字符构成
int fail[MAXN];//fail指针,失配后跳转到fail指针指向的节点
int cnt[MAXN];
int num[MAXN];
int len[MAXN];//len[i]表示节点i表示的回文串的长度
int S[MAXN];//存放添加的字符
int last;//指向上一个字符所在的节点,方便下一次add
int n;//字符数组指针
int p;//节点指针
int newnode(int l) {//新建节点
for (int i = 0; i < N; ++i)
next[p][i] = 0;
cnt[p] = 0;
num[p] = 0;
len[p] = l;
return p++;
}
void init() {//初始化
p = 0;
newnode(0);
newnode(-1);
last = 0;
n = 0;
S[n] = -1;//开头放一个字符集中没有的字符,减少特判
fail[0] = 1;
}
int get_fail(int x) {//和KMP一样,失配后找一个尽量最长的
while (S[n - len[x] - 1] != S[n])
x = fail[x];
return x;
}
int add(int c) {
c -= 'a';
S[++n] = c;
int ct = 0;
int cur = get_fail(last);//通过上一个回文串找这个回文串的匹配位置
if (!next[cur][c]) {//如果这个回文串没有出现过,说明出现了一个新的本质不同的回文串
int now = newnode(len[cur] + 2);//新建节点
fail[now] = next[get_fail(fail[cur])][c];//和AC自动机一样建立fail指针,以便失配后跳转
next[cur][c] = now;
num[now] = num[fail[now]] + 1;
ct = num[now];
}
last = next[cur][c];
cnt[last]++;
return num[last];
}
void count() {
for (int i = p - 1; i >= 0; --i)
cnt[fail[i]] += cnt[i];
//父亲累加儿子的cnt,因为如果fail[v]=u,则u一定是v的子回文串!
}
}