AC自动机

发表于 | 分类于 ， | 阅读次数：
本文字数： 4k | 阅读时长 ≈ 4 分钟

AC自动机用途

给多个字符串t，再询问一个字符串s，问有多少个字符串t出现在询问的字符串s中。

前置技能

学AC自动机之前，先学会什么是字典树，什么是kmp。kmp我写过一篇博客，就不讲了，就是next 数组保存一个最长匹配前缀。字典树就更简单了，每个节点从根节点开始，出现一个字符就在父亲节点上连上下一个节点，也不多说。有需要再写一篇博客。

AC自动机

对于这个玩意，都说是字典树上跑KMP,到也没错。朴素KMP是在一个串上面跑next,而AC自动机只是变成了在字典树节点上跑fail指针，每个fail指针保存是最长匹配后缀。推荐一名大佬博客，讲的挺不错的。
朴素的写法，每一个字符串t对s做一次kmp算法或者 对所有的t字符串建一颗字典树，然后每个位置匹配一下，很显然$O(n^2)$的复杂度，绝对超时。
仔细思考一下，字典树里面，每次匹配都要从下一个位置开始跑一次匹配，类比一下没有kmp的朴素字符串匹配。是不是有点相似。普通单个字符串匹配，是不是枚举每一个位置，然后做一次暴力匹配？然后kmp 做了什么，通过next找到最大匹配前缀。那么我们是否可以在字典树用fail保存最大匹配后缀呢？显然是可以的，不然AC自动机干啥.
举个栗子： 假设有三个t asa aaa aas, 匹配aasab
字典树建成这个样子，丑了点，别在意，重在思想。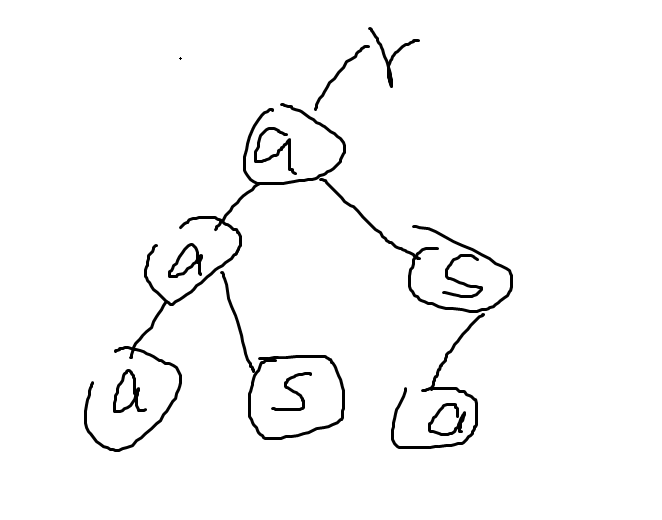

然后一开始吧aas匹配掉了没啥意见吧，然后继续匹配aasa，很显然这个时候没有这个字符串，那么肯定就要转移，
转移到哪去呢？最长匹配后缀啊。如图是不是这样。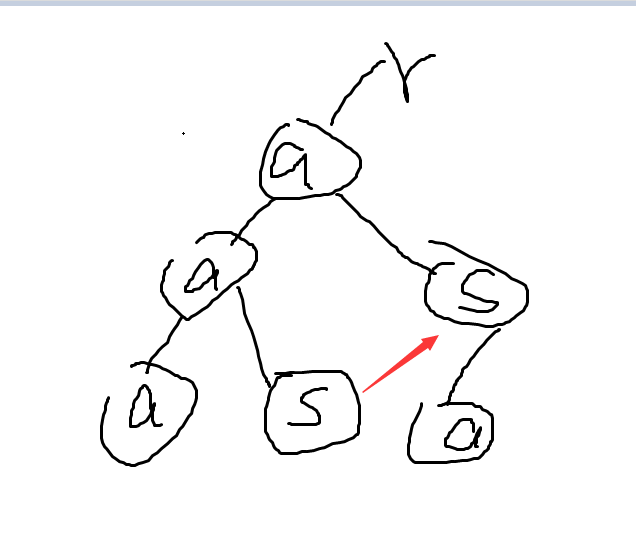

然后匹配asa,再继续匹配b,很显然失配了啊，然后找最长匹配后缀，只有根节点了，然后根节点背后又没有b。所以啥都没了，匹配最长后缀为空串。
好了，现在差不多理解这个算法的思想，接下来就是一些细节，不知道我还有没有没有考虑到的，如果有请在评论区提问。
1.上诉所讲的例子很明显，aas向as跳转，如果后继没有a这个节点怎么办?asa 改成asb,asa要匹配谁呢？这个在kmp算法里面也有这个问题，很显然，继续找下去就能解决问题，假设 再加一个tsb，aasb适配，aas调转到as没有后继b,再跳转到匹配后缀s，有后继b就匹配sb，类推，如果还没有找到就继续想上找。ps: 这个地方可以优化，fail指针找到了最长匹配后缀，然后字典树的下一个节点可以直接跳到对应位置如例子 aas后继a可以直接跳到为asa这个节点，不过不优化也没啥影响，因为字符串长度是固定的，最多不会跳超过n次，不优化只是多了个常数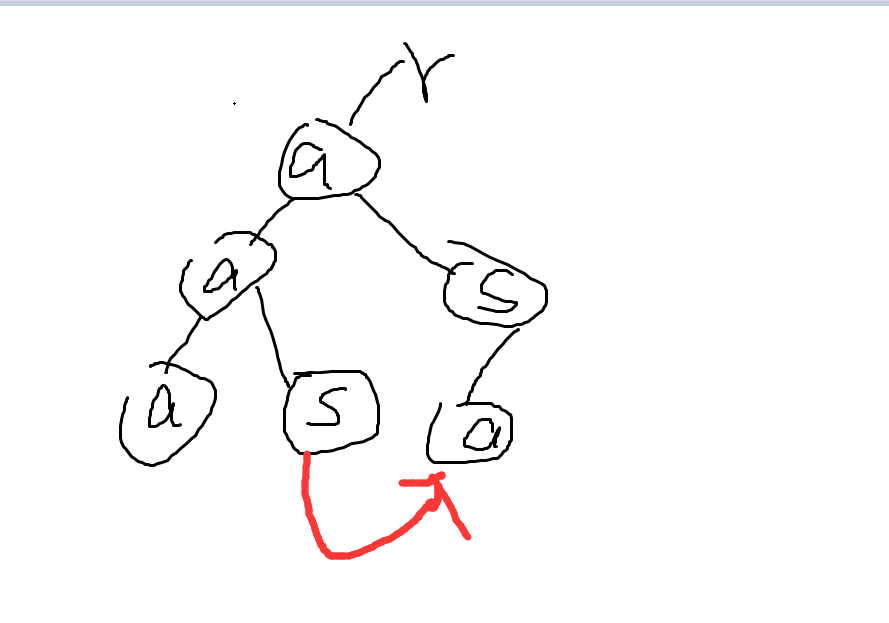
2.多个匹配怎么办？没到一个节点把他的fail找下去记录个数，如图字典树匹配sa,的时候会找他的fail,找到a然后把a这个节点记录，同理找sab,不仅仅把自己匹配了，还要把b匹配掉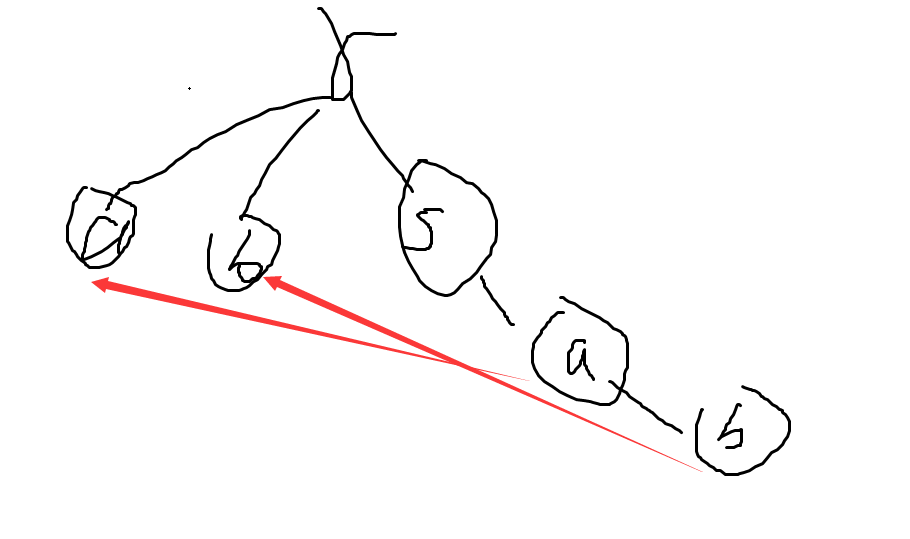
3.怎么记录个数，如果一个字符串多次出现怎么办，看代码，记录一下就行了。

这个AC自动机的思想还是要学好，后面回文自动机要用到这个玩意的思想。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
namespace Aho_Corasick_Automaton {
int trie[maxn][27];  //字典树
int cntword[maxn];   //记录单词出现次数，可以开一个vector记录是第几个单词
int fail[maxn];     // 失败回溯
int cnt=0;          // 树的节点个数

void init(int x) {
    for(int i=0; i<26; i++) {
        trie[x][i]=0;
    }
}

void insertWords(char *s) {
    int ls=strlen(s);
    int root=0;
    for(int i=0; i<ls; i++) {
        int next=s[i]-'a';
        if(!trie[root][next]) {
            init(++cnt);
            trie[root][next]=cnt;
        }
        root=trie[root][next];
    }
    cntword[root]++;
}

void getFial() {
    queue<int> q;
    for(int i=0; i<26; i++) {
        if(trie[0][i]) {
            fail[trie[0][i]]=0;
            q.push(trie[0][i]);
        }
    }
    while(q.size()) {
        int now=q.front();
        q.pop();

        for(int i=0; i<26; i++) {
            if(trie[now][i]) {
                fail[trie[now][i]]=trie[fail[now]][i];
                q.push(trie[now][i]);
            } else
                trie[now][i]=trie[fail[now]][i];
        }
    }

}

int query(char *s) {
    int ls=strlen(s);
    int now =0,ans=0;
    for(int i=0; i<ls; i++) {
        now=trie[now][s[i]-'a'];
        for(int j=now; j&&cntword[j]!=-1; j=fail[j]) {
            // 如果这种状态已经计算过了就不用继续找下去了
            ans+=cntword[j];//统计个数，可以在这进行各种操作
            cntword[j]=-1;
        }
    }
    return ans;
}
}

再贴一个大哥板子

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
queue<int>q;
struct Aho_Corasick_Automaton {
    int c[N][26],val[N],fail[N],cnt;
    void ins(char *s) {
        int len=strlen(s);
        int now=0;
        for(int i=0; i<len; i++) {
            int v=s[i]-'a';
            if(!c[now][v])
                c[now][v]=++cnt;
            now=c[now][v];
        }
        val[now]++;
    }
    void build() {
        for(int i=0; i<26; i++)
            if(c[0][i])
                fail[c[0][i]]=0,q.push(c[0][i]);
        while(!q.empty()) {
            int u=q.front();
            q.pop();
            for(int i=0; i<26; i++)
                if(c[u][i])
                    fail[c[u][i]]=c[fail[u]][i],q.push(c[u][i]);
                else
                    c[u][i]=c[fail[u]][i];
        }
    }
    int query(char *s) {
        int len=strlen(s);
        int now=0,ans=0;
        for(int i=0; i<len; i++) {
            now=c[now][s[i]-'a'];
            for(int t=now; t&&~val[t]; t=fail[t])
                ans+=val[t],val[t]=-1;
        }
        return ans;
    }
} AC;