2019 Multi-University Training Contest 4-1003 Divide the Stones

发表于 | 分类于 ， | 阅读次数：
本文字数： 3.9k | 阅读时长 ≈ 4 分钟

HDU 6616 Divide the Stones
题意： 给一个n和一个k，将重量为[1,n]的石子分成k堆，每堆重量一样。
题解： 先将石子分成n/k份，比如15 3，分成
1 2 3
4 5 6
7 8 9
10 11 12
13 14 15
不难看出如果刚好偶数分，每两份组成一个，分配一定是刚好分配合理的，比如上述例子没有13 14 15,肯定是前两组分成 1 6,2 5 3 4 后两组7 12 8 11 9 10,这样一定是平分的。
如果是奇数，>3的份数，依旧一样的处理，1 2 3前三份再分成3等份。这个分法有很多，我找了一个比较辣鸡的。 画个图给你看下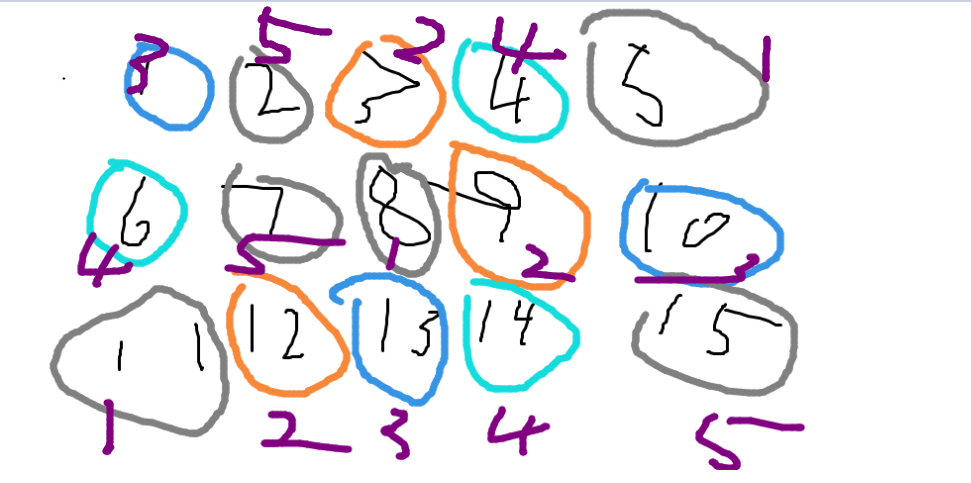

图给你了，看不看得懂就是你的悟性了，告辞.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
#include "bits/stdc++.h"

using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int, int> P;
#define VNAME(value) (#value)
#define bug printf("*********\n");
#define debug(x) cout<<"["<<VNAME(x)<<" = "<<x<<"]"<<endl;
#define mid (l + r) / 2
#define chl 2 * k + 1
#define chr 2 * k + 2
#define lson l, mid, chl
#define rson mid + 1, r, chr
#define pb push_back
#define mem(a, b) memset(a, b, sizeof(a));


const LL mod = (LL) 1e9 + 7;
const int maxn = (int) 1e6 + 5;
const int INF = 0x7fffffff;
const LL inf = 0x3f3f3f3f;
const double eps = 1e-8;
#ifndef ONLINE_JUDGE
clock_t prostart = clock();
#endif

void f() {
#ifndef ONLINE_JUDGE
    freopen("../data.in", "r", stdin);
#endif
}

LL n, k;
vector<int> v[maxn];
vector<LL> ans[maxn];

int main() {
    int T;
    f();
    scanf("%d", &T);
    while (T--) {
        scanf("%lld%lld", &n, &k);
        LL sum = n * (n + 1) / 2 / k;
        if (n == 1 && k == 1) {
            puts("yes\n1");
            continue;
        }
        if (n == k || n * (n + 1) / 2 % k != 0) {
            puts("no");
        } else if (k == 1) {
            puts("yes");
            for (int i = 1; i <= n; i++) {
                printf("%d%c", i, i == n ? '\n' : ' ');
            }
        } else {
            n /= k;
            int pos = 1;
            for (int i = 1; i <= n; i++) {
                for (int j = 0; j < k; j++) {
                    v[i].push_back(pos++);
                }
            }
            puts("yes");
            if (n & 1) {
                for (int j = 4; j <= n; j += 2) {
                    for (int i = 0; i < k; i++) {
                        ans[i].push_back(v[j][i]);
                        ans[i].push_back(v[j + 1][k - i - 1]);
                    }
                }
                int j = k / 2 - 1;
                for (int i = 0; i < k; i++) {
                    ans[i].push_back(v[3][i]);
                    ans[i].push_back(v[2][(++j) % k]);
                }
                for (int i = 0; i < k; i++) {
                    LL temp = 0;
                    for (int j = 0; j < n; j++) {
                        if (j + 1 != n)temp += ans[i][j];
                        else ans[i].push_back(sum - temp);
                        printf("%lld", ans[i][j]);
                        if (j + 1 == n)printf("\n");
                        else printf(" ");
                    }
                    ans[i].clear();
                }

            } else {
                for (int j = 1; j <= n; j += 2) {
                    for (int i = 0; i < k; i++) {
                        ans[i].push_back(v[j][i]);
                        ans[i].push_back(v[j + 1][k - i - 1]);
                    }
                }

                for (int i = 0; i < k; i++) {
                    for (int j = 0; j < n; j++) {
                        printf("%lld", ans[i][j]);
                        if (j + 1 == n)printf("\n");
                        else printf(" ");
                    }
                    ans[i].clear();
                }
            }

        }
        for (int i = 0; i <= n; i++) {
            v[i].clear();
        }
    }
    return 0;
}