单调栈和单调队列

发表于 | 更新于 | 分类于 ， | 阅读次数：
本文字数： 4.2k | 阅读时长 ≈ 4 分钟

理解单调栈和单单调队列之前，要明白一种技巧，叫做尺取法。

尺取法

尺取法，两个位置，一个是l，一个r,r一位位的左移，l根据条件左移。比如POJ 3061
求最大连续字串和不超过s
l r初始化为0,r左移，总和加上r位置的值，如果总和一旦大于s,l开始左移，直到满足[l,r]区间的总和小于s，这种通过l,r反复推进的方法，就叫尺取法。

细心的人可以发现，这种方法，求结果一定要满足，右边一个位置跨过r到l一定是不合法的的情况。

单调栈

其实这个和尺取法关系不大。。。。
单调栈,用于求最左边（右边）的第一个满足某种具有单调性质条件（比如大于，小于）的位置。
距离，求第一个大于的位置。求大于，将不大于的数全部加入单调栈里面，保证栈单调递减，（下面距离栈中存的是小标,注意区分值和下标）
假设有1 3 5 2 1 4 7 6
一开始栈为空，将第一个数位置加进去，此时栈中有下标1
到第二个数 3 ，栈顶 位置的值 小于3弹出，赋值位置右边第一个大于他的数下标是2，然后栈为空，将2号位置加入栈，依次类推.
到5 弹出下标2 加入下标3,到 2 因为栈顶位置的值大于2不弹出，直到4 弹出值2,1，不弹出5。
当前值比栈顶的数大，弹出栈顶的值，并赋值，否则加入栈。

单调队列

单调队列和尺取法用点像，和单调栈也差距不大。总结来说，位置尺取，队列单调，就想尺取法和单调栈的结合体。例子 HDU 3530
按题目来讲： 查寻区间最大最小值之差在[m,k]之间的最大长度。
现按照尺取的方法来：不断移动，l，r,虽然从在r右边跨过r 到l 最大最小值之差绝对是大于等于[r,l]之间的,但是最大最小不可能一直是端点，可能[r,l]之间存在比r,l大或者小的值。那么该如何处理呢，单调栈可以保存一个单调的子序列，我们是否能和他一样保存[l,r],的单增子序列呢？很显然是可以的。因为我们的[l,r]有两端，所以用栈是肯定不行的，那么就只能用双端队列。我们建立两个双端队列，一个保存[l,r]递增的子序列，一个保存[l,r]递减的子序列，那么递减队列中第一个值保存的就是[l,r]区间的最大值，递增的就是最小值。那么假设[l,r] 区间的最大值和最小值不满足条件了，要尺取就要移动l,怎么移动？我们要改变最大最小值。改变哪里一个？肯定是离r最远的那一个，我们单调队列保存的下标，直接把l移动到两个队列队首，最小的下标+1,然后弹出队首，就相当于找到了新[l,r]最大（最小）值 (因为我们队列是单调的，弹出了最大（最小）值就相当于找到了次大（次小）值，在新区间就没有比他小的了 ) 然后，一直循环直到满足条件为止。
单增队列就是队尾进，每次和单调栈一样保证队列中是单调的，队首永远都是最小的或者最大的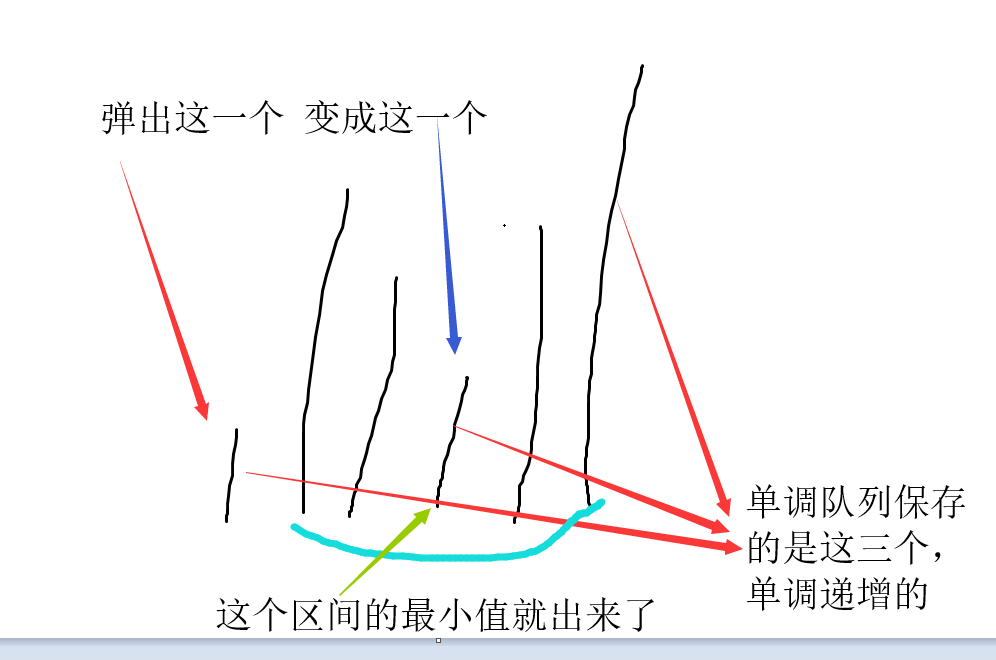

HDU 3530 AC代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
#include "bits/stdc++.h"

using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int, int> P;
#define VNAME(value) (#value)
#define bug printf("*********\n");
#define debug(x) cout<<"["<<VNAME(x)<<" = "<<x<<"]"<<endl;
#define mid (l + r) / 2
#define chl 2 * k + 1
#define chr 2 * k + 2
#define lson l, mid, chl
#define rson mid + 1, r, chr
#define pb push_back
#define mem(a, b) memset(a, b, sizeof(a));


const LL mod = (LL) 1e9 + 7;
const int maxn = (int) 1e6 + 5;
const int INF = 0x7fffffff;
const LL inf = 0x3f3f3f3f;
const double eps = 1e-8;
#ifndef ONLINE_JUDGE
clock_t prostart = clock();
#endif

void f() {
#ifndef ONLINE_JUDGE
    freopen("../data.in", "r", stdin);
#endif
}

struct deq {
    static const int start = maxn * 2;
    int dat[start * 2];
    int l = start;
    int r = start;

    void push_front(int x) {
        dat[l--] = x;
    }

    void pop_front() {
        l++;
    }

    int front() {
        return dat[l + 1];
    }

    void push_back(int x) {
        dat[++r] = x;
    }

    void pop_back() {
        r--;
    }

    int back() {
        return dat[r];
    }

    int size() {
        return r - l;
    }

    void clear() {
        r = l = start;
    }

    bool empty() {
        return r == l;
    }
};

deque<int> dq, dq2;


int n, m, k;
int a[maxn];

int main() {
    f();
    while (~scanf("%d%d%d", &n, &m, &k)) {
        int ans = 0;
        dq.clear();
        dq2.clear();
        int pos = 0;
        for (int i = 1; i <= n; i++) {
            scanf("%d", &a[i]);
            // 大的弹出所以最前面是最小的
            while (dq.size() > 0 && a[dq.back()] > a[i]) {
                dq.pop_back();
            }

            dq.push_back(i);
            while (dq2.size() > 0 && a[dq2.back()] < a[i]) {
                dq2.pop_back();
            }
            dq2.push_back(i);
            while (a[dq2.front()] - a[dq.front()] > k) {
                if (dq2.front() < dq.front()) {
                    pos = dq2.front();
                    dq2.pop_front();

                } else {
                    pos = dq.front();
                    dq.pop_front();
                }
            }
            if (dq2.size() && dq.size() && a[dq2.front()] - a[dq.front()] >= m) {
                ans = max(ans, i - pos);
            }
        }
        printf("%d\n", ans);
    }
#ifndef ONLINE_JUDGE
    cout << "运行时间:" << 1.0 * (clock() - prostart) / CLOCKS_PER_SEC << "s\n";
#endif // ONLIN_JUDGE
    return 0;
}
/*
5
4
 */

友情提示：最好别用 std 里面的栈和队列，太慢了
进阶题：2019牛客暑期多校训练营（第三场）F Planting Trees
题解 ： 2019牛客暑期多校训练营（第三场）F Planting TreesF/)