2019 Multi-University Training Contest 2 1012 Longest Subarray

发表于 | 更新于 | 分类于 ， | 阅读次数：
本文字数： 7.2k | 阅读时长 ≈ 7 分钟

Longest Subarray HDU 6602

题意: n个数，求区间内 数的个数要么为0个要么大于等于k个的长度最长是多少。
题解：
解法一： 不完美算法，每次枚举计算区间内所有数的个数有多少个，如果没有数的个数小于k的就更新答案,如果有就把这几个数标记，然后这些数会把原本的数组分成几段，然后在这几段中继续求。
理论上这种写法会超时，实际上就是超时了，所以我们把分的次数限定一下，如果分了超过30次就直接跳出。这样理论上没有把所有可能性跑到，但是这种数据很难得，所以只要没有专门卡这种数据就能过。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
#include "bits/stdc++.h"

using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int, int> P;
#define VNAME(value) (#value)
#define bug printf("*********\n");
#define debug(x) cout<<"["<<VNAME(x)<<" = "<<x<<"]"<<endl;
#define mid (l + r) / 2
#define chl 2 * k + 1
#define chr 2 * k + 2
#define lson l, mid, chl
#define rson mid + 1, r, chr
#define pb push_back
#define mem(a, b) memset(a, b, sizeof(a));


const LL mod = (LL) 1e9 + 7;
const int maxn = (int) 1e6 + 5;
const int INF = 0x7fffffff;
const LL inf = 0x3f3f3f3f;
const double eps = 1e-8;
#ifndef ONLINE_JUDGE
clock_t prostart = clock();
#endif

void f() {
#ifndef ONLINE_JUDGE
    freopen("../data.in", "r", stdin);
#endif
}

int n, c, k;

int a[maxn];
int b[maxn];
int pos = 0;
int v[maxn];
int ans = 0;
int de[maxn];

int dfs(int l, int r, int dep) {

    if (dep > 30)return 0;
    if (r < l)return 0;
    if (r - l + 1 < k)return 0;
    for (int i = l; i <= r; i++) {
        b[a[i]] = 0;
    }
    pos = 0;
    for (int i = l; i <= r; i++) {
        if (b[a[i]] == 0) {
            v[pos++] = a[i];
        }
        b[a[i]]++;
    }
    int flag = 0;
    for (int i = 0; i < pos; i++) {
        if (b[v[i]] >= k) {
            b[v[i]] = 1;
        } else {
            b[v[i]] = 0;
            flag = 1;
        }
    }
    for (int i = l; i <= r; i++) {
        if (b[a[i]] == 0)de[i] = 0;
        else de[i] = 1;
    }
    if (flag == 0) {
        ans = max(ans, r - l + 1);
        return 0;
    }
    int L = -1, R = -1;
    for (int i = l; i <= r; i++) {
        if (de[i] && L == -1) {
            L = i;
        }
        if (de[i] == 0 && L != -1) {
            R = i - 1;
            dfs(L, R, dep + 1);
            L = -1;
        }
    }
    if (L != -1 && L <= r) {
        dfs(L, r, dep + 1);
    }
}

int main() {
    f();
    while (~scanf("%d%d%d", &n, &c, &k)) {
        ans = 0;
        for (int i = 1; i <= n; i++)scanf("%d", &a[i]);
        dfs(1, n, 0);
        printf("%d\n", ans);
    }
#ifndef ONLINE_JUDGE
    cout << "运行时间:" << 1.0 * (clock() - prostart) / CLOCKS_PER_SEC << "s\n";
#endif // ONLIN_JUDGE
    return 0;
}

题解二： 枚举区间r,线段树查找最小的l。
能够选的位置一定是分成两段。然后把从 r到l 少于k个数字不合法 区间 -1，变成合法的时候+1，大于等于0的区间中最小下标就是答案。
假设，k=3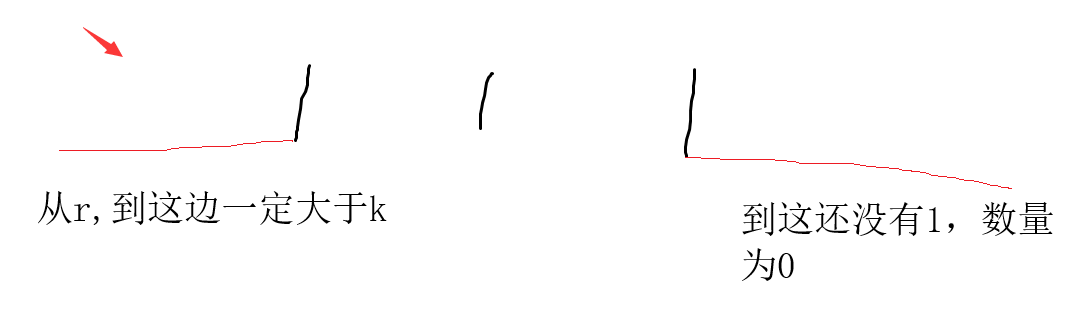

每个数字一定是这样，举个例子
k=2
1 4 1 4 2 1 1
首先到 r=1 a[r]=1 ,没有超过 k个, 把 最开始到 r 全部减 1
-1
查询 [1,r] 没有大于等于0的位置，不更新答案
r=2 a[r]=4 ,个数少于 k,[1,r] -1
-2 -1
[1,r] 没有大于0 的位置 ,不更新
r=3 a[r]=1 ,大于等于 k 个，把当前位置和前面a[r]位置之间 -1, 也就是 [2,3] -1 ,然后超过k个的位置 [1,1] +1
-1 -2 -1
还是没有0的位置 不更新
r=4 a[r]=4，同上[3,4] -1 ，[1,2] +1
0 -1 -2 -1
最小0位置为1 pos=1 更新答案 ans=max(ans,r-pos+1)
后面依次类推

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
#include "bits/stdc++.h"

using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int, int> P;
#define VNAME(value) (#value)
#define bug printf("*********\n");
#define debug(x) cout<<"["<<VNAME(x)<<" = "<<x<<"]"<<endl;
#define mid (l + r) / 2
#define chl 2 * k + 1
#define chr 2 * k + 2
#define lson l, mid, chl
#define rson mid + 1, r, chr
#define pb push_back
#define mem(a, b) memset(a, b, sizeof(a));


const LL mod = (LL) 1e9 + 7;
const int maxn = (int) 1e6 + 5;
const int INF = 0x7fffffff;
const LL inf = 0x3f3f3f3f;
const double eps = 1e-8;
#ifndef ONLINE_JUDGE
clock_t prostart = clock();
#endif

void f() {
#ifndef ONLINE_JUDGE
    freopen("../data.in", "r", stdin);
#endif
}

int n, c, k;

int a[maxn];
int ans = 0;
int last[maxn];
int b[maxn];
int dat[maxn << 2];
int lazy[maxn << 2];
int lastk[maxn], pre[maxn], nxt[maxn];

void build(int l, int r, int k) {
    if (r == l) {
        dat[k] = 0;
        lazy[k] = 0;
    } else {
        build(lson);
        build(rson);
        dat[k] = 0;
        lazy[k] = 0;
    }
}

void push_down(int l, int r, int k) {
    if (r == l)dat[k] += lazy[k];
    else {
        lazy[chl] += lazy[k];
        lazy[chr] += lazy[k];
    }
    lazy[k] = 0;
    if (r != l)dat[k] = max(dat[chl] + lazy[chl], dat[chr] + lazy[chr]);
}

void update(int A, int B, int l, int r, int k, int x) {
//    if (k == 0) {
//        printf("[%d,%d] %d\n", A, B, x);
//    }
    push_down(l, r, k);
    if (A > r || B < l)return;
    else if (A <= l && r <= B) {
        lazy[k] += x;
    } else {
        update(A, B, lson, x);
        update(A, B, rson, x);
        dat[k] = max(dat[chl] + lazy[chl], dat[chr] + lazy[chr]);
    }
}

int query(int A, int B, int l, int r, int k) {
    push_down(l, r, k);
    if (A > r || B < l || dat[k] < 0)return inf;
    else if (r == l && A <= l && r <= B) {
        return l;
    } else {
        if (B <= mid || dat[chl] + lazy[chl] >= 0) {
            return query(A, B, lson);
        } else return query(A, B, rson);
    }
}

int queryval(int A, int B, int l, int r, int k) {
    push_down(l, r, k);
    if (A > r || B < l)return -inf;
    else if (A <= l && r <= B) {
        return dat[k];
    } else {
        return max(queryval(A, B, lson), queryval(A, B, rson));
    }
}

int main() {
    f();
    while (~scanf("%d%d%d", &n, &c, &k)) {
        ans = 0;
        build(1, n, 0);
        for (int i = 0; i <= c; i++)b[i] = last[i] = lastk[i] = pre[i] = nxt[i] = 0;
        for (int i = 1; i <= n; i++) {
            scanf("%d", &a[i]);
            nxt[last[a[i]]] = i;
            pre[i] = last[a[i]];
            if (b[a[i]] + 1 >= k) {
                update(pre[i] + 1, i, 1, n, 0, -1);
                update(pre[lastk[a[i]]] + 1, lastk[a[i]], 1, n, 0, 1);
                lastk[a[i]] = nxt[lastk[a[i]]];
            } else if (b[a[i]] == 0) {
                update(1, i, 1, n, 0, -1);
                lastk[a[i]] = i;
                pre[i] = 0;
            } else if (b[a[i]] + 1 < k) {
                update(last[a[i]] + 1, i, 1, n, 0, -1);
            }
            last[a[i]] = i;
            ans = max(ans, i - query(1, i, 1, n, 0) + 1);
            b[a[i]]++;
        }
        if (k == 1)ans = n;
        else if (k == 0)ans = 0;
        printf("%d\n", ans);
    }
#ifndef ONLINE_JUDGE
    cout << "运行时间:" << 1.0 * (clock() - prostart) / CLOCKS_PER_SEC << "s\n";
#endif // ONLIN_JUDGE
    return 0;
}