NTT
理解了FFT的原理,NTT也差不多。FTT是用复数实现变换,而NTT是用取模意义实现。
找出一个g,和开一个模数p,g是p的原根。
原根 $0<i<P,0<j<P,1<g<P\ g^i(mod\ p)\ne g^j(mod\ p)$
这样在FTT里面的$w_n^1\equiv g^{\frac{p-1}{n}}$。
显然:
$(g^\frac{p-1}{n})^n=g^{p-1}=1(mod\ p)$
$g^\frac{p-1}{n} * g^\frac{p-1}{n} = g^{2\frac{p-1}{n}}$
同样的 FFT 里面用到的几个原根性质,他都有。
你可以抽象为,把一个长度为 P 线段,每次走一格,走了N次回来了。
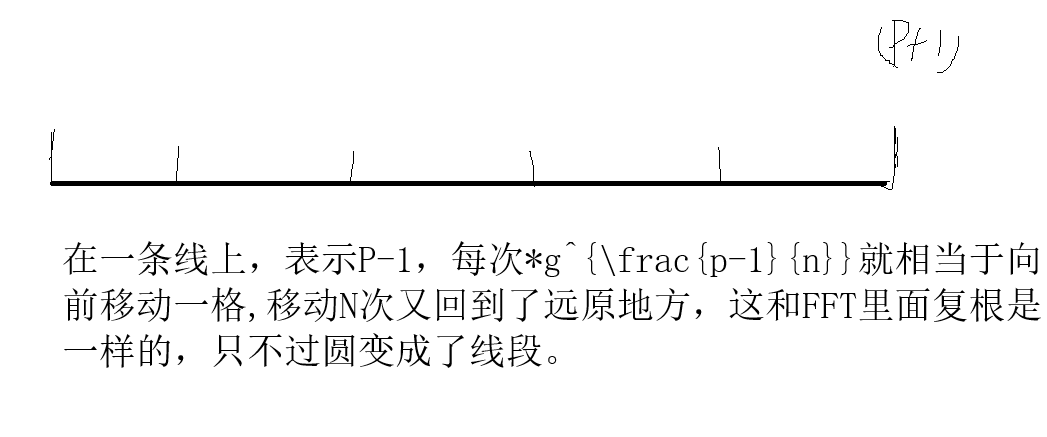
所以一开始要求的几个点值是
$\{A(1),A(g^{\frac{p-1}{n}}),\cdots,A(g^{\frac {p-1}{n}{n-1}})\}$1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114//ntt
using namespace std;
typedef long long ll;
const int N=(1<<18)+5, INF=1e9;
const double PI=acos(-1);
inline int read(){
char c=getchar();int x=0,f=1;
while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
return x*f;
}
ll P=1004535809;
ll Pow(ll a, ll b,ll P) {
ll ans=1;
for(; b; b>>=1, a=a*a%P)
if(b&1) ans=ans*a%P;
return ans;
}
struct NumberTheoreticTransform {
int pow2(int x) {
int res = 1;
while (res < x)
res <<= 1;
return res;
}
inline LL pow_mod(ll x, int n) {
ll res;
for (res = 1; n; n >>= 1, x = x * x % mod)
if (n & 1)
res = res * x % mod;
return res;
}
inline int add_mod(int x, int y) {
x += y;
return x >= mod ? x - mod : x;
}
inline int sub_mod(int x, int y) {
x -= y;
return x < 0 ? x + mod : x;
}
void NTT(LL a[], int n, int op) {
for (int i = 1, j = n >> 1; i < n - 1; ++i) {
if (i < j)
swap(a[i], a[j]);
int k = n >> 1;
while (k <= j) {
j -= k;
k >>= 1;
}
j += k;
}
for (int len = 2; len <= n; len <<= 1) {
LL g = pow_mod(3, (mod - 1) / len);
for (int i = 0; i < n; i += len) {
LL w = 1;
for (int j = i; j < i + (len >> 1); ++j) {
LL u = a[j], t = 1ll * a[j + (len >> 1)] * w % mod;
a[j] = (u + t) % mod, a[j + (len >> 1)] = (u - t + mod) % mod;
w = 1ll * w * g % mod;
}
}
}
if (op == -1) {
reverse(a + 1, a + n);
LL inv = pow_mod(n, mod - 2);
for (int i = 0; i < n; ++i)
a[i] = 1ll * a[i] * inv % mod;
}
}
void mul(LL A[], LL B[], int Asize, int Bsize) {
int n = pow2(Asize + Bsize - 1);
for (int i = Asize; i < n; ++i)
A[i] = 0;
for (int i = Bsize; i < n; ++i)
B[i] = 0;
NTT(A, n, 1);
NTT(B, n, 1);
for (int i = 0; i < n; ++i) {
A[i] = 1ll * A[i] * B[i] % mod;
B[i] = 0;
}
NTT(A, n, -1);
return;
}
} f;
int n1, n2, m, c[N];
ll a[N], b[N];
char s1[N], s2[N];
int main() {
//freopen("in","r",stdin);
scanf("%s%s",s1,s2);
n1=strlen(s1); n2=strlen(s2);
for(int i=0; i<n1; i++) a[i] = s1[n1-i-1]-'0';
for(int i=0; i<n2; i++) b[i] = s2[n2-i-1]-'0';
m=n1+n2-1;
f.mul(a, b, m);
for(int i=0; i<m; i++) c[i]=a[i];
for(int i=0; i<m; i++) c[i+1]+=c[i]/10, c[i]%=10;
if(c[m]) m++;
for(int i=m-1; i>=0; i--) printf("%d",c[i]);
}