FFT快速傅里叶变换简解

发表于 | 更新于 | 分类于 ， | 阅读次数：
本文字数： 9.8k | 阅读时长 ≈ 9 分钟

概述

FTT： 快速傅里叶变换。看起来挺难的，实际上确实挺难的。

用途

求

也就是上面两个多项式相乘等于下面这个

朴素算法一个个乘 $O(n^2)$ 复杂度，FFT能在 $O(nlog(n)$ 的复杂度内解决。

点值

这个是多项式 系数表达

下面这个是 点值表示法

不难看出能用下面这个n+1个不同的点值推出 系数表达式

FFT步骤

  1. 加倍次数界求值 将转A B系数表达式，找出 2n+1 个点值,(只需要n+1个点值就能推出一个最高次项为n的表达式，但是，A B相乘后有2n，所以要找出2n+1个值)
  2. 逐点相乘 将两个点值相乘获得C 的点值
  3. 插值 再用逆变换将C的点值转换成 系数表达式

第一步叫离散傅里叶变换 (DFT)

正式讲解

不难看出,如果直接用朴素算法，去求多项式乘积，第一步复杂度 $O(n^2)$,第二步$O(n)$，第三步$O(n^2)$
FFT 作用就是优化第一步和第三步，都变成$O(nlog(n))$的复杂度。

在这之前需要知道一个东西叫单位复根

单位复根

不具体讲了,讲了你也理解不了。 (其实我没理解)
想要具体了解见黑书算法导论P532，我只做简介
n次单位复根，$w^n=1$，这个数有恰好n个，具体是啥不重要，我说个简单的理解。
复数大家都知道吧。
假设有两个复数
$z1=a+bi$
$z2=c+di$
把他们两个乘一下

求一下$z1 z2$他们的长度和角，
先求长度

是不是就等于$[z1] * [z2]$
然后你代一个数放z1 z2里面

看到这应该懂了，复数的乘法性质。

可能你还不知道这意味着啥，但是马上你就懂了
假设一个复数，长度为1，角度为，$w_n^1=cos(\frac{2\pi}{n})+sin(\frac{2\pi}n{})i$
把他画成成圆就是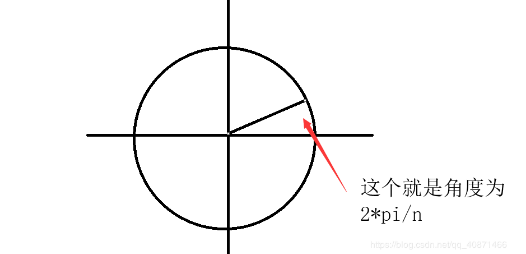

那么 就相当于在圆上转了一下
如下图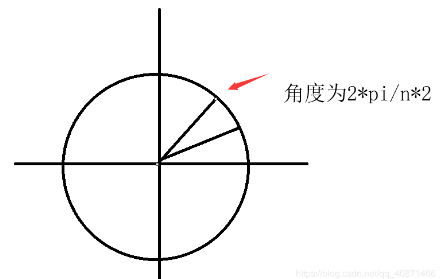

看到这，后面理解性质就贼简单，你全部想象成在圆上面旋转。但是这些都不重要接下来给你退公式了,假设 A有最高次项为 n-1

可以发现前面一堆和后面一堆很像
然后设这$A0 A1$

这个地方注意，A0,A1 里面的次项是开根号
所以是
假设你代入的是一个普通的数，假设是 ，$A(X)=A0(X^2)+xA1(X^2)$ 你还需要求 ,一共是2n个，两边同时求还是$O(n)$.
当你带入复数 ,你可以发现一个神奇的事，要求的数量变少了

上述公式化简用上了一个公式

这个事很显然的事，在单位圆里面，改变这个比例，角度不变

你需要求的数就变成了看上去没有减少，实际上你可以发现，其中有一半其实是重复的，这又要立用到一个公式

$w_n^k=w_n^{k+n}$ 很显然，圆转了一圈，我又回来啦

所以就变成了求
举个栗子 解释一下
假设 一个 A长度为4 最高次项就是 3
求 4 个 点值

一开始要求的有 4 个点值
通过前面那个转换, 看不懂为啥有个1的 ，注意 $w_n^0=1$

要求的点值就变成了$\{A0(1),A0(w_2^1),A1(1),A1(w_2^1)\}$ 同样是4个， 但是递归下去找每次分成两部分，就相当于折半了，(还是没有理解等会画个图给你看下)
另外还没完，上述还有一个特点: 前面一半和后面一半 很像，没错，还可以优化。这个地方又要用到一个性质.

$w_n^{k+\frac{n}{2}}=-w_n^{k}$ 很显然,你在圆里面转了半圈，不就是个相反的了么。。。。

感觉我的证明都是显然证明法,不用在意这些细节
由此可以再优化
当$k<\frac{n}{2}$

当$k>\frac{n}{2}$

网上很多写的是，其实是一个意思，哪个好理解你看哪个吧。
例子对应上面举得那个具体的例子，你就可以再次优化了。

这个地方看不懂推荐一篇神级大佬的博客 从多项式乘法到快速傅里叶变换

最后再画个图助解一下:


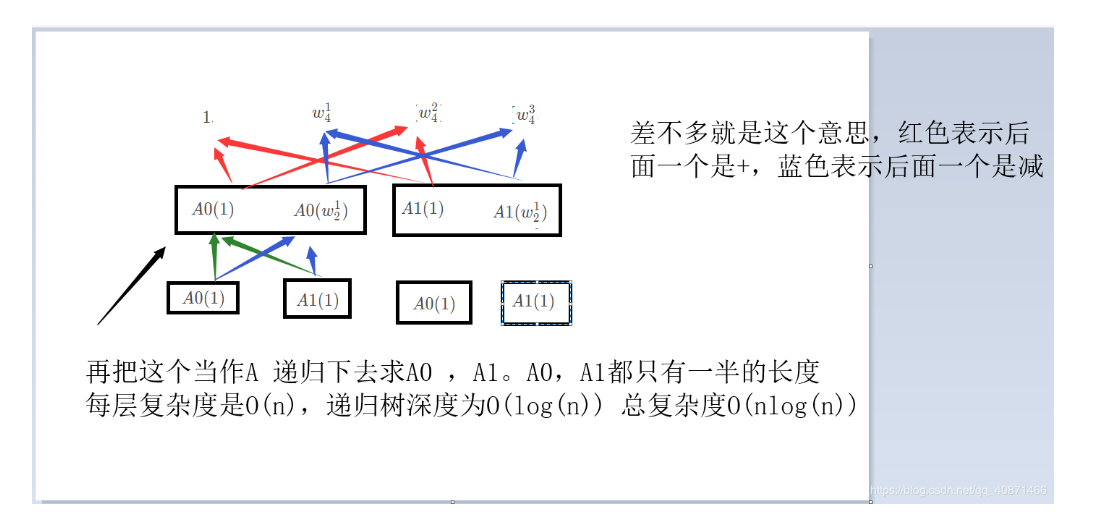
至此算法核心原理全部解释完毕。逆运算从点值 转换成系数表达式 ，你把矩阵写出来，就相当于乘了一个逆矩阵。就相当于再求一次DFT ，只不过 $w_n^k$ 变成他的逆，，加个负号就行了。
代码网上一大堆我这里贴个我的，测试题目
51Nod 大数乘法2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
#include "bits/stdc++.h"

using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int, int> P;
#define VNAME(value) (#value)
#define bug printf("*********\n");
#define debug(x) cout<<"["<<VNAME(x)<<" = "<<x<<"]"<<endl;
#define mid (l + r) / 2
#define chl 2 * k + 1
#define chr 2 * k + 2
#define lson l, mid, chl
#define rson mid + 1, r, chr
#define pb push_back
#define mem(a, b) memset(a, b, sizeof(a));


const LL mod = (LL) 1e9 + 7;
const int maxn = (int) 1e6 + 5;
const int INF = 0x7fffffff;
const LL inf = 0x3f3f3f3f;

#ifndef ONLINE_JUDGE
clock_t prostart = clock();
#endif

void f() {
#ifndef ONLINE_JUDGE
    freopen("../data.in", "r", stdin);
#endif
}

const double eps = 0.5;
const double pi = acos(-1.0);

struct complexx {
    double x, y;

    complexx(double xx = 0, double yy = 0) { x = xx, y = yy; }

    void put() {
        printf("[x=%f y=%f]\n", x, y);
    }
} a[maxn], b[maxn];

complexx operator+(complexx a, complexx b) { return complexx(a.x + b.x, a.y + b.y); }

complexx operator-(complexx a, complexx b) { return complexx(a.x - b.x, a.y - b.y); }

complexx operator*(complexx a, complexx b) { return complexx(a.x * b.x - a.y * b.y, a.y * b.x + a.x * b.y); }

void fft(int len, complexx *a, int o) {
    if (len == 1) return;
    complexx a0[(len >> 1) + 3], a1[(len >> 1) + 3];
    for (int i = 0; i <= len; i += 2)
        a0[i >> 1] = a[i], a1[i >> 1] = a[i + 1];
    fft(len >> 1, a0, o);
    fft(len >> 1, a1, o);
    complexx wn = complexx(cos(2 * pi / len), o * sin(2 * pi / len)), w0 = complexx(1, 0);
    for (int i = 0; i < (len >> 1); i++, w0 = w0 * wn) {
        a[i] = a0[i] + w0 * a1[i];
//        a[i + (len >> 1)] = a0[i] - w0 * a1[i];  //前面说的一个优化
    }
    //不加优化继续跑下去，直接枚举所有
    for (int i = (len >> 1); i < len; i++, w0 = w0 * wn) {
        a[i] = a0[i - (len >> 1)] + w0 * a1[i - (len >> 1)];
    }

}

char s[maxn];
int ans[maxn];

int main() {
    f();
    scanf("%s", s);
    int la = strlen(s);
    for (int i = la - 1; i >= 0; i--)a[i].x = s[la - i - 1] - '0';
    scanf("%s", s);
    int lb = strlen(s);

    for (int i = lb - 1; i >= 0; i--)b[i].x = s[lb - i - 1] - '0';
    int m = la + lb - 2;
    int len = 1;

    for (; len <= m; len <<= 1);
    fft(len, a, 1);//DFT
    fft(len, b, 1);//DFT
    for (int i = 0; i <= len; i++)
        a[i] = a[i] * b[i];
    fft(len, a, -1);//IDFT
    for (int i = 0; i <= m; i++) {
        ans[i] = (int) (a[i].x / len + eps);//记得除len eps 用来消 浮点误差我用的 0.5
    }
    for (int i = 0; i <= m; i++)ans[i + 1] += ans[i] / 10, ans[i] = ans[i] % 10;
    if (ans[m + 1])printf("%d", ans[m + 1]);
    for (int i = m; i >= 0; i--) {
        printf("%d", ans[i]);
    }
    puts("");
#ifndef ONLINE_JUDGE
    cout << "运行时间:" << 1.0 * (clock() - prostart) / CLOCKS_PER_SEC << "s\n";
#endif // ONLIN_JUDGE
    return 0;
}

你以为大结局了吗?没有

优化

除了前面那个直接再表达式上的优化,，下面还有代码上的优化。
递归太慢了，可以换成迭代。另外，这空间变成了nlog(n) ，那个辅助数组优化掉也可以不好.
已经理解核心了，后面这个就不用我说了吧。。。。。。是我懒得写了，我18岁我好累

直接贴一个大哥的板子把，找的太多了都不知道是谁的了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
//fft
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
typedef long long ll;
const int N=(1<<18)+5, INF=1e9;
const double PI=acos(-1);
inline int read(){
    char c=getchar();int x=0,f=1;
    while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
    while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
    return x*f;
}
 
struct meow{
    double x, y;
    meow(double a=0, double b=0):x(a), y(b){}
};
meow operator +(meow a, meow b) {return meow(a.x+b.x, a.y+b.y);}
meow operator -(meow a, meow b) {return meow(a.x-b.x, a.y-b.y);}
meow operator *(meow a, meow b) {return meow(a.x*b.x-a.y*b.y, a.x*b.y+a.y*b.x);}
meow conj(meow a) {return meow(a.x, -a.y);}
typedef meow cd;
 
struct FastFourierTransform {
    int n, rev[N];
    cd omega[N], omegaInv[N];
    void ini(int lim) {
        n=1; int k=0;
        while(n<lim) n<<=1, k++;
        for(int i=0; i<n; i++) rev[i] = (rev[i>>1]>>1) | ((i&1)<<(k-1));
        
        for(int k=0; k<n; k++) {
            omega[k] = cd(cos(2*PI/n*k), sin(2*PI/n*k));
            omegaInv[k] = conj(omega[k]);
        }
    }
    void fft(cd *a, cd *w) {
        for(int i=0; i<n; i++) if(i<rev[i]) swap(a[i], a[rev[i]]);
        for(int l=2; l<=n; l<<=1) {
            int m=l>>1;
            for(cd *p=a; p!=a+n; p+=l) 
                for(int k=0; k<m; k++) {
                    cd t = w[n/l*k] * p[k+m];
                    p[k+m]=p[k]-t;
                    p[k]=p[k]+t;
                }
        }
    }
    void dft(cd *a, int flag) {
        if(flag==1) fft(a, omega);
        else {
            fft(a, omegaInv);
            for(int i=0; i<n; i++) a[i].x/=n;
        }
    }
    void mul(cd *a, cd *b, int m) {
        ini(m);
        dft(a, 1); dft(b, 1);
        for(int i=0; i<n; i++) a[i]=a[i]*b[i];
        dft(a, -1);
    }
}f;
 
int n1, n2, m, c[N];
cd a[N], b[N];
char s1[N], s2[N];
int main() {
    //freopen("in","r",stdin);
    scanf("%s%s",s1,s2);
    n1=strlen(s1); n2=strlen(s2);
    for(int i=0; i<n1; i++) a[i].x = s1[n1-i-1]-'0';
    for(int i=0; i<n2; i++) b[i].x = s2[n2-i-1]-'0';
    m=n1+n2-1;
    f.mul(a, b, m);
    for(int i=0; i<m; i++) c[i]=floor(a[i].x+0.5);
    for(int i=0; i<m; i++) c[i+1]+=c[i]/10, c[i]%=10;
    if(c[m]) m++;
    for(int i=m-1; i>=0; i--) printf("%d",c[i]);
}

如有错误，望指出。