2019牛客暑期多校训练营(第一场) C Euclidean Distance

发表于 | 更新于 | 分类于 ， | 阅读次数：
本文字数： 2.6k | 阅读时长 ≈ 2 分钟

2019牛客暑期多校训练营（第一场）C Euclidean Distance

题解: 拉格朗日乘子法，首先引入拉格朗日乘子得出公式

这个应该看的懂，然后引入对偶变成成其中

然后化成叉姐给的题解里面的公式就行了

再然后，我就不会了qaq
后来看了一下别的大佬的博客，突然感觉可以直接理解一下，
假设所有的$p_i=0$,$f(x)$就等于$a_i^2$的和


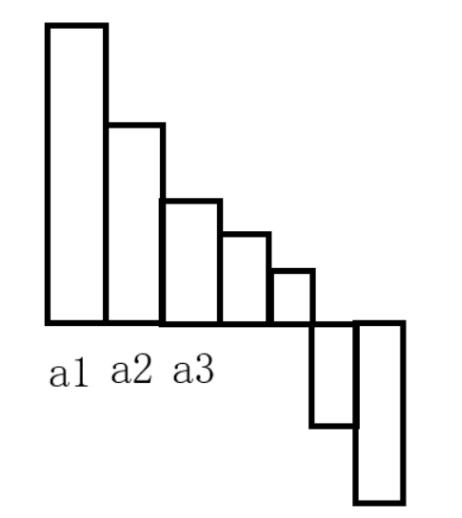
题目要求的是 在

条件下求 $f(x)=\sum_{i=1}^{n}(p_i-a_i)^2$ 。相当于分配$p_i$ 的值，去让 $(p_i-a_i)^2$ 变小。
根据二次函数的性质，自变量 $x$ 越大因变量 $y$ 化越快。所以先分配给最大肯定更优啊，直接贪心下去啊。最后肯定是变成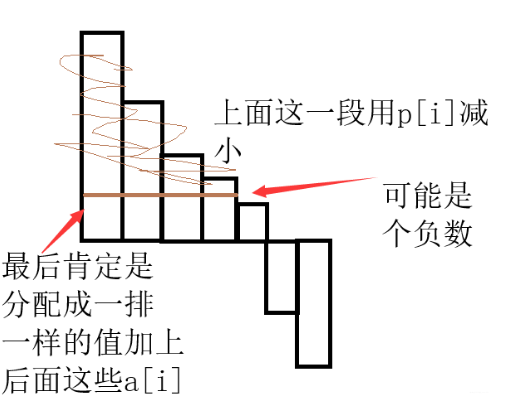

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
#include<iostream>
#include<algorithm>
#include<cstring>
#include<string>
#include<vector>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<queue>
#include<map>
#include<set>
#include<stack>
#include<bitset>

using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int,int> P;

#define VNAME(value) (#value)
#define bug printf("*********\n");
#define debug(x) cout<<"["<<VNAME(x)<<" = "<<x<<"]"<<endl;
#define mid (l+r)/2
#define chl 2*k+1
#define chr 2*k+2
#define lson l,mid,chl
#define rson mid+1,r,chr
#define pb push_back
#define mem(a,b) memset(a,b,sizeof(a));

const long long mod=1e9+7;
const int maxn=1e6+5;
const int INF=0x7fffffff;
const LL inf=0x3f3f3f3f;
const double eps=1e-8;
void f() {
#ifndef ONLINE_JUDGE
    freopen("dat.in", "r", stdin);
#endif // ONLIN_JUDGE
}

LL a[maxn];
int n;
LL m;
int main() {
    while(~scanf("%d%lld",&n,&m)) {
        for(int i=1; i<=n; i++) {
            scanf("%lld",&a[i]);
        }
        sort(a+1,a+n+1,greater<int>());
        LL r=m;   //p[i]的总分配价值是 1  也就是 m/m
        LL pos=1; // pos 标记能够分配p[i] 到第 pos 个
        while(pos<n) {
            if(r<(a[pos]-a[pos+1])*pos)break;
            r-=(a[pos]-a[pos+1])*pos;
            pos++;
        }
        // 最终前pos个的值  都会是a[pos]-r/pos,将他扩大pos 倍, 然后再乘以 pos 个
        LL ans=(a[pos]*pos-r)*(a[pos]*pos-r)*pos;       //因为最后的值可能是 1/pos,所以把分子分母同时乘以pos个
        LL b=m*m*pos*pos;       // 因为求的是距离的平方 分母 就是 m*m*pos*pos
        for(int i=pos+1; i<=n; i++) { //分配不到的 a[i]，直接加上
            ans+=a[i]*a[i]*pos*pos;
        }
        LL g=__gcd(ans,b);
        if(ans%b==0)printf("%lld\n",ans/b);
        else printf("%lld/%lld\n",ans/g,b/g);
    }
    return 0;
}